Ejercicios Resueltos de Mecánica (Solucionario)
Ejercicios, Soluciones y Bibliografías
para abrir una imagen en tamaño completo puedes hacer clic derecho sobre la imagen, y en el menú elegir alguna de las opciones para abrir imagen; o bien guardarla.
Ejercicios resueltos, 1 y 2 en la imagen de abajo:
1-Determinar el alargamiento total de una barra de acero de 60cm. De longitud si la fatiga de extensión es igual a 1.000 kg/cm2.
E = 2,1 x 10^6 Kg/cm^2
2.- Determinar la fuerza total de extensión de una varilla cilíndrica de acero de 2 cm. De diámetro si el alargamiento unitario es igual a 0.7 X 10-3

Solución a ejercicio 5 y 6 en las imágenes más abajo.
5 - Determinar el diámetro d de los pernos de acero de una prensa para un esfuerzo máximo P= 50.000 kg si el coeficiente de trabajo para el acero en este caso es de 1000 kg/cm. Determinar el alargamiento total de los pernos para la carga máxima, si la longitud entre sus cabezas es de 1,50 m
solución extendida en imagen más de abajo (escaneo)
6- Una estructura está formada por dos barras iguales de acero (fig. 4) de 4,50 m. de longitud, cuyos extremos están sometidos a la acción de una carga vertical P. Determinar la sección recta de la barra y el descenso vertical del punto B para P = 2.500 kg. a, = 800 kg/ cm. ‘ y ul Ángulo inicial de inclinación de Las barras, 30°
solución a los dos anteriores aquí:
Fuente:

respuesta:
1 - Un poste corto construido con un tubo circular hueco de aluminio, soporta una carga de compresión de 26 kips. Los diámetros interior y exterior del tubo son d1 = 4 in y d2 = 4,5 in, respectivamente y su longitud es 16 in. El acortamiento del poste debido a la carga es de 0,012 in. Determine el esfuerzo de compresión. No considere el peso del poste y suponga que no se pandea con la carga.
2 - Una barra circular de acero con longitud L y diámetro d cuelga en el tiro de una mina y en su extremo inferior un balde con mineral con peso W. Obtenga una formula para el esfuerzo máximo σmax en la barra, tomando en cuenta el peso de ésta. Calcule el esfuerzo máximo si L = 40 m, d = 8 mm y W = 1,5 kN
3 - Un tubo de acero de Longitud L = 4,00 ft, diámetro exterior d 2 = 6,00 in. Y
diámetro interior d1= 4,5 in., está comprimido por una fuerza axial P = 140 k.
El material tiene un módulo de elasticidad E = 30000 ksi y una razón de
Poisson ν = 0,30
Determinar las siguientes características del tubo :
* Su alargamiento.
* La deformación unitaria lateral.
Solución de los ejercicios:
El 3 a mitad de la hoja


estos se resolvieron más arriba

1.2.2 Un ciclista aplica una fuerza P de 70 N al freno de mano frontal de una bicicleta (P es la resultante de una presion distribuida uniformemente). Conforme el freno de mano gira en A, se desarrolla una tension T en el cable con longitud de 460 mm (Ae = 1.075 mm2) que se estira en d = 0.214 mm. Determine el esfuerzo normal y la deformacion unitaria en el cable del freno.
Respuesta a mitad de la hojas:

La armadura de dos barras ABC que se muestra en la figura, tiene soportes articulados en los puntos A y C, que están separados 2.0 m. Los elementos AB y BC son barras de acero, interconectadas por un pasador en el nodo B. La longitud de la barra BC es de 3 m. Un anuncio que pesa 5.4 KN está suspendido de la barra BC en los puntos D y E, en los puntos que están ubicados a 0.8 m y 0.4 m, respectivamente, de los extremos de la barra. Determine el área de la sección transversal necesaria de la barra AB y el diámetro necesario del pasador en el soporte C. Si los esfuerzos permisibles en tensión y cortante son 125 MPa y 45 MPa, respectivamente (nota: los pasadores en los soportes están en cortante doble. Además no tome en cuenta los pesos de los elementos AB y BC
a mitad de la hoja se encuentra el ejercicio resuelto de la barra ABC

Un poste circular hueco ABC soporta una carga P1=1500 lb que actúa en su parte superior. Una segunda carga P2 está distribuida uniformemente alrededor de la placa de cubierta del poste en B. El diámetro y el espesor de las partes superior e inferior del poste son:
dbAB= 1.50 in, tAB =0.275 in, dBC=2.00 in y tBC=0.275 in, respectivamente.
a. Calculen el esfuerzo normal σAB en la parte superior del poste.
1415 Lbs/Pulg2
b. Si se desea que la parte inferior del poste tenga el mismo esfuerzo de comprensión que la parte superior, ¿cuál será la magnitud de la carga P2?
608 Lbs/Pulg2
c. Si P1 permanece en 1500 lb y P2 ahora se fija en 2000 lb, ¿qué espesor nuevo de BC resultará en el mismo esfuerzo de comprensión en las dos partes?
.54 Pulg
Solución al ejercicio:

Un puntal S de acero que sirve como riostra a un malacate marino transmite una fuerza P
de compresión de 54 kN a la plataforma de un muelle. El puntal tiene una sección
transversal cuadrada hueca con espesor de pared t = 12 mm y el ángulo θ entre el puntal y
la horizontal es de 40º. Un pasador que atraviesa al puntal trasmite la fuerza de compresión
del puntal a dos placas de unión G soldadas a la placa de base B. Cuatro pernos de anclaje
la aseguran a la plataforma. El diámetro del pasador es dpas = 18 mm, el pasador de las
placas de unión es tG = 15 mm, el espesor de a placa de base es tB = 8 mm y el diámetro de
los pernos de anclaje es dperno = 12 mm.
Determinar los siguientes esfuerzos: a) el esfuerzo de aplastamiento entre el puntal y el
pasador; b) el esfuerzo cortante en el pasador; c) el esfuerzo de aplastamiento entre el
pasador y las placas de unión; d) el esfuerzo de aplastamiento entre el anclaje y la placa de
base, y e) el esfuerzo cortante en los pernos de anclaje. (Despréciese cualquier fricción
entre la placa de base y la plataforma).
Ejercicio Hecho a mitad de la hoja:

El ejercicio del cartel (letrero) que cuelga está hecho más arriba.
Una barra de acero que trabaja como barra de suspensión para maquinaria pesada en una fábrica, está acoplada a un soporte mediante la conexión con perno. La parte principal del colgante tiene una sección transversal rectangular con un ancho b1= 1.5 in y un espesor t = 0.5 in. En la conexión con el perno la barra de suspensión se ensancha hasta un ancho b2= 3.0 in. El perno, que transFere la carga de la barra a las dos placas de unión, tiene un diámetro d =1.0 in
Determine el valor permisible de la carga de tensión P en la barra de suspensión con base en las siguientes consideraciones:(a) El esfuerzo de tensión permisible en la parte principal de la barra de suspensión es 16,000 psi.(b) El esfuerzo de tensión permisible en la barra de suspensión en su sección transversal que pasa por el agujero del perno es 11,000 psi. (El esfuerzo permisible en esta sección es menor debido a las concentraciones de esfuerzos alrededor del agujero).(c) El esfuerzo de apoyo permisible entre la barra de suspensión y el perno es 26,000 psi.(d) El esfuerzo cortante permisible en el perno es 6500 psi.
El ejercicio resuelto comienza a mitad de la hoja:

1 - Considerar la unión atornillada de la figura. La fuerza es de 3.000 kg y el diámetro del perno de 1,2 cm. Determinar el valor medio de las tensiones cortantes que existen en cada uno de los pernos a-a y b-b
respuesta al ejercicio en la imagen de arriba
2 -en el ejercicio anterior si la carga máxima de trabajo cortante es de 1000 kg/cm. Determinar el diámetro del perno necesario para no exceder este valor.
resolución del ejercicio en la imagen de arriba
3 - Considerar un perno de acero de 1 cm de diámetro y sometido a una carga de tracción axial de 1.000 kg, como se representa en el esquema adjunto. Determinar la tensión cortante media en la cabeza del perno suponiendo que el cortante actúa sobre una superficie cilíndrica del mismo diámetro que el perno, como se indica por las líneas de trazos.
Solución al ejercicio en la imagen de arriba

4 - La fuerza P tiende a cortar el tope a lo largo del plano a-a. Si P = 4.000 kg, determinar la tensión cortante media en el plano a-a.
respuesta al ejercicio en la imagen de arriba y en
http://es.slideshare.net/miguelsalazarcayo/resistencia-materiales-53855883 (slide 28 - 29 - 30)
5 - Habitualmente, se unen entre sí los árboles y las poleas por medio de una chaveta, como se ve en la Fig. (a). Considerar una polea sometida a un momento de giro T de 11.000 cm-kg enclavada con una chaveta de 1,2 x 1,2 x 7,5 cm a un árbol. Determinar la tensión cortante en un plano horizontal a través de la chaveta.
respuesta al ejercicio en la imagen de arriba y en
6 - Se ha usado un punzón circular de 2 cm de diámetro para punzonar un agujero en una chapade 12 mm de espesor. Si la fuerza necesaria para el punzón atraviese el metal fue de 30.000 kg,determinar la tensión cortante máxima producida en el material.
Solución a ejercicio:
o en
7 - En las estructuras se usan muchas veces apoyos de angulares de acero para transferir cargas de vigas horizontales a pilares verticales. Si la reacción de la viga sobre el angular es una fuerza,dirigida hacia abajo, de 5.000 kg, como se ve en la figura, y si esta fuerza la resiste dos roblones de 2,2 cm de diámetro, hallar la tensión cortante media en cada uno de ellos.
resolución de este ejercicio en la imagen de arriba
8 - Muchas veces se usa el dispositivo de la figura para determinar la resistencia a cortante en una unión encolada. Si la carga P de la rotura es de 1.200 kg, ¿ cuál es la tensión cortante media en la unión de este instante?.
Ejercicio hecho en la imagen de más abajo y también en:
(bajar para ver)
9 - La probeta se sujeta entre los tacos A1, A2 y B1, B2 y se aplica una fuerza P dirigida hacia abajo en el taco C, como se muestra en la figura. ¿Qué fuerza hay que aplicar para romper una barra redonda de acero laminado en caliente de 20 mm de diámetro y que tiene una resistencia última a corte de 7.300 [kg/cm2]?
ejercicio resuelto en la imagen de abajo
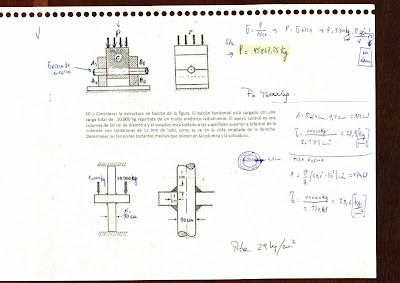
considerar la estructura de balcón de la figura. El balcón horizontal está cargado con una carga total de 10.000 kg repartida de un modo simétrico radialmente. El apoyo central es una columna de 50 cm de diámetro y el voladizo está soldado a las superficies superior e inferior de la columna con soldadura de 1 mm de lado. como se ve en la vista ampliada de la derecha.
Determinar las tensiones cortantes medias que existen en la columna y la soldadura.
Ver imagen de arriba con ejercicio resuelto.

Ejercicios de Torsión resueltos:
1 - Dimensionar un eje de sección circular llena de longitud L que se encuentra solicitado por un par torsor Mt. Determinar los ángulos de torsión total y unitario.
L = 3 m, Mt = 4000 daN cm, Tau admisible = 800 daN/cm^2, G = 800.000 daN/cm^2
Solución al ejercicio en la imagen a continuación:

Ejercicios de Flexión resueltos:
1 - Determinar la tensión máxima del eje de locomotora si c = 35 cm, el diámetro d del eje es de 25 cm y la carga P e nel extremo es de 13.000 kg.
Solución al ejercicio en la imagen de abajo
2- Determinar el radio de curvatura r y la flecha del eje del problema anterior si el material es acero y la distancia entre los centros de apoyo es 150 cm.
Respuesta a como hacer el ejercicio en la imagen de abajo
3 - Un perfil comercial de 30 cm está apoyado como indica la figura y cargado en los voladizos con una carga uniformemente distribuida de 1000 kg/cm. Determinar la tensión máxima en la parte central de la viga, si momento de inercia es 9785 cm^4. Determinar la flecha en su punto medio.
ejercicio resuelto aquí abajo
Atención: